If the brain were so simple we could understand it, we would be so simple we couldn't. Lyall Watson
To preserve the speed advantage of our neural network chip, the used evolutionary training algorithm must be implemented in a way, that it can keep pace with the speed of the networks. Within our group, an evolutionary coprocessor has been developed, that provides efficient means to accelerate the algorithm by executing the necessary genetic operations within a configurable logic (FPGA).
Using the coprocessor for the genetic manipulations, the speed of the algorithm is now potentially limited by its remaining parts. These are basically the selection procedure and the calculation of each network's fitness with respect to its response to the training data. To facilitate a fast implementation of these parts, they are preferably kept simple. However, while the restriction to simple selection schemes and fitness functions warrants the effective exploitation of the speed of the network chip, it poses a new problem: It is not at all self-evident that complex neural networks can successfully be trained for real-world applications using only simple algorithms.
Therefore, one main topic of our current research on evolutionary network training is the design of new learning strategies that allow to use even simple but fast evolutionary algorithms to efficiently train the complex neural networks that are implementable on the chip.
One natural way to solve a complicated problem by simple means is to divide it into several, easier to solve parts and tackle these tasks independently or at least sequentially. Transferred to neural networks, this corresponds to building the complete network from several smaller networks that each solve a different subproblem of the task in question and that can be trained separately.
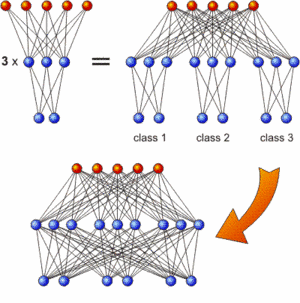 The incremental training strategy: First train subnetworks which are then combined and interconnected
The incremental training strategy: First train subnetworks which are then combined and interconnected
A typical kind of tasks that are commonly solved by artificial neural networks are classification problems: A number of instances - each described by a set of feature values - has to be correctly allocated to one of several classes. A large number of classification tasks have their origin in the biomedical field. The specific problem could be to predict from what kind of disease a patient is suffering, what type of protein a sequence of DNA is coding or where in the cell a given protein is localized.
A classification task with N classes can easily be divided into N problems with only one class each where the network merely has to decide whether an instance belongs to this respective class or not. As all these networks process the same input features, they can be regarded as subnetworks of one large network that solves the whole task. This is schematically depicted in the upper half of the image for only three classes and rather simple networks. In a second step (bottom half of the image), the subnetworks can be interconnected and the additional synaptic weights can be evolved while the connections within the subnetworks remained fixed.
All of the learning steps - the training of the subnetworks and the training of the connections between them - address comparably easy subproblems of the whole task and therefore allow the use of simple but fast algorithms. It can be shown that - following an incremental learning strategy like the one described above - our neural network chip can successfully be trained for realistic problems. For example, a common ten-fold cross-validation experiment on the well-known problem of the cellular localization sites of E.coli proteins yields an averaged generalization success rate of approx 83%. This is competitive to the results of other classification systems which range from 81% to 86%.
For the above results, the trained networks have been implemented on one single network chip. They contain one hidden layer with 56 inner neurons (7 per class) and are distributed over two of the four available network blocks. The networks have been trained using the Hannee software package developed in our group and can be visualized using the included HNetDataEditor. Click on the thumbnails below to get an impression of what a completely evolved network looks like.
 Screenshot 1: (Click on image to enlarge) Within the weight matrix display of the HNetDataEditor (right half of the window), positive weights are a shade of blue while negative weights are red. White squares correspond to zero weights, i.e., non-existing connections. This image shows the enlargement of the first used network block which contains the first layer of the network. Note, that the connections to the input neurons are multi-bit integer connections with a precision of 6 bit.
Screenshot 1: (Click on image to enlarge) Within the weight matrix display of the HNetDataEditor (right half of the window), positive weights are a shade of blue while negative weights are red. White squares correspond to zero weights, i.e., non-existing connections. This image shows the enlargement of the first used network block which contains the first layer of the network. Note, that the connections to the input neurons are multi-bit integer connections with a precision of 6 bit.
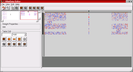 Screenshot 2: (Click on image to enlarge) This image shows the second used network block of the example individual. It contains the second layer of the network and thus also shows the interconnections between the several subnetworks (see above). Some of the weights that correspond to such interconnections remained zero after training. The correct classification of the corresponding class did obviously not require connections to the hidden neurons of the other subnetworks.
Screenshot 2: (Click on image to enlarge) This image shows the second used network block of the example individual. It contains the second layer of the network and thus also shows the interconnections between the several subnetworks (see above). Some of the weights that correspond to such interconnections remained zero after training. The correct classification of the corresponding class did obviously not require connections to the hidden neurons of the other subnetworks.
As can be seen from the above screenshots, the resulting networks are already quite complex. However, they do not even completely occupy two blocks of one network chip. In future investigations, it is planned to address more complicated problems that have to be solved by larger networks distributed on several chips and that might require extended training strategies.
Electronic Vision(s) Group – Dr. Johannes Schemmel
Im Neuenheimer Feld 227
69120 Heidelberg
Germany
phone: +49 6221 549849
fax: +49 6221 549839
email: schemmel(at)kip.uni-heidelberg.de
How to find us