Real-world problems usually are described by continuous quantities. This continuity can only be efficiently handled by digital data processing systems when the variables are quantized with a certain accuracy. With the commonly used data types of 8, 16, 32bit it is possible to represent 256, 65536 and 232 ~4,3*109 different values respectively. In today's digital computers (PCs) 32bit data types come at no extra cost and provide sufficient accuracy in most cases.
In highly parallel hardware implementations, on the other hand, the accuracy provided by each computational element has a non-neglectable impact on the overall size and power consumption of the system, thus limiting the achievable complexity. When analog electronics come into play, one further has to consider that the reachable accuracy is inherently limited and the effort for higher accuracies grows exceedingly.
Two design goals of the HAGEN neural network chip were high parallelism while maintaining scalability: the network model was chosen as to allow for a good integration density and a feasible interfacing scheme. These considerations led to a network of McCulloch-Pitts neurons (threshold neurons with binary inputs and outputs) connected by analog synapses (10bit+sign). This is not only efficient in terms of silicon usage, but also allows to use problem dependent coding schemes. In turn this means that one has to think about the coding when the inputs or outputs of the network are not binary.
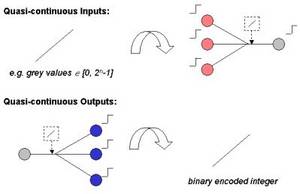
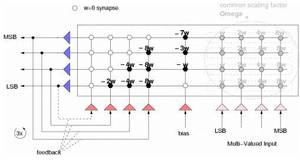
The solution to the problem of interfacing multi-valued signals to a network with binary inputs and outputs is the following: For multi-valued inputs one considers n binary input neurons to form a group encoding an n-bit integer. The integer value then needs to be translated into an analog network activity according to the significance of the representing bits. The least significant bit (LSB) induces ω, the next bits 2ω, 22ω and so on. The most significant bit (MSB) induces 2n-1ω into the network. This is a digital-to-analog conversion. The actual weight of the multi-valued input now is a common scaling factor, Ω. Similar to the combination of binary input neurons for multi-valued inputs it is possible to group elementary output neurons to act as an m-bit integer output. The task to be performed by this group of neurons is to measure the analog network activity present at their inputs and represent this activity as an integer. They act as analog-to-digital converters (ADCs). This can be realized by configuring a recurrent network topology with self-inhibiting feedback connections acting as a successive approximation ADC. The proposed solution imposes two conditions: First, the participating output neurons need to be excited by the same analog activity and, second, the analog activity has to stay stable over the course of the successive approximation. One important prerequisite of the above approaches is the homogeneity of the network's elementary elements (synapses and neurons), since several of them get combined and precalculated weights are used. This contrasts the almost inevitable property of analog circuits: their inhomogeneity in space (fabrication effects) and time (fluctuations, noise). With the chosen network model though it is possible to account for the static deviations with a simple offset correction for each neuron. The necessary calibration data is measured separately and the offsets are compensated for transparently. More details on this calibration process can be found in the publication 'A Mixed-Mode Analog Neural Network using Current-Steering Synapses' (HD-KIP-03-05).
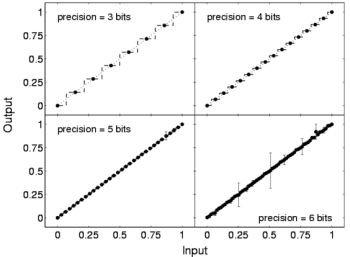
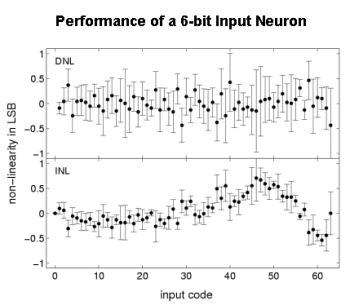
It was successfully shown that it is possible to obtain multi-valued inputs of up to 6-bit precision with a calibrated HAGEN chip. The figure on the right shows plots of the commonly used performance measures differential non-linearity (DNL) and integral non-linearity (INL) versus the applied input code for a group of 6 neurons acting as a multi-valued input. Since the DNL is always smaller than 1 LSB, the monotonicity of the DAC is guaranteed. In practice, not only a single multi-valued input is needed but rather several of them. Measurements show that a sufficient precision for 6-bit inputs across a network block is reached.
The figure on the left shows the network output of several analog to digital conversions for 3, 4, 5 and 6-bits. The above setup was used, i.e., the network activity was induced by the according multi-valued inputs. The error bars resemble the standard deviation of the repetitive measurements. The performance of the ADCs is almost perfect up to 5 bits. In the 6-bit case there are deviations of a few LSB for input codes where the MSB or the second most important bit turns on and the lower bits go off.
The proposed approaches show the feasibility of the suggested variable coding with binary neurons. It even allows to allocate exactly as much accuracy as needed to certain parts of the network according to the problem. For an example see the 'Predicting Protein Cellular Localization Sites with a Hardware Analog Neural Network' (HD-KIP-03-15).
HOME
